Everyone knows the must-have Tier 1 FPP at Epcot is the Character Spot. Everyone should make that their number 1 priority!
Hmm. I don’t think the math on that is going to pencil out.
You’ve missed two of my favorites. Those are must do’s every trip. People Mover day and night.
Some people think 7DMT is boring, but I LOVE it! I can’t do the fast/rough roller coasters like EE or RNRC… they hurt my head. But 7DMT has the thrill of a fast roller coaster, but it is smooth smooth and sways side to side.
MV3D: my 16yo son actually LOVED this attraction. It was so creative and funny and I thought the animatronics and effects were very well done.
MTP = Mad Tea Party (the teacups… surprised they did NOT make me nauseated!)
PCRC = Prince Charming’s Regal Carousel
Gotcha!
I’m excited to ride 7DMT & SDD because I think my spine can handle both of those. (I ruptured a disc on The Drop Zone at Great America so no jerky rides for moi). I think swaying sounds okay. I do have the Carousel penciled in, too! It’s just so classic.
The only one I don’t have room for at this time is MTP, which I’m not sure we’ve ever ridden. I think they’re going to extend park hours on one of the days we’re at MK (Sat. on Memorial Day weekend) so that one could go there. I’m not sure I’d do it but the rest of the family could.
I charge by the hour.
That’s about how long I had to spend with my DS16 last night going over trigonometry. Wonder what he owes me.
ETA: I spent a good deal of time trying to explain the difference between an inverse function, versus just an inverse. He was confused that arctan isn’t the same as tan^-1, or cot. I said, “cotangent is the inverse of tangent, not the inverse FUNCTION of tangent”, etc. Finally found the right explanation and all become clear to him!
This would be me.
Lies
Please enjoy it, then. I’ll be queing for a coaster that’s actually thrilling.
Yes, mathematical notation can be ambiguous and inconsistent. For example 3(a+b) = 3a+3b. What about k(a+b)? Does that equal ka+kb? Maybe, maybe not. If k is a constant it does, but k might be a function, in which case it does not.
Incidentally, I’d prefer to say that cot(x) is the reciprocal of tan(x) rather than the inverse.
Which reminds me, here’s another inconsistency: how do you pronounce cot(x)? Like “cott”, right? Because that’s how it’s written. But it’s short for cotangent, so surely it should be pronounced “coat”?
Think I’m crazy? How do you pronounce sin(x)? See: inconsistent!
Actually, no. Always pronounced it like “coat”. That’s how I was taught it as well. But that could very well be a regional thing.
Yes. This makes sense. Trouble is, the curriculum he is using used the term “inverse”, so I was trying to get him to understand the difference between just “inverse” versus “inverse function”. If the curriculum had just used reciprocal, it would have been far less confusing!
My realisation that we are inconsistent with the pronunciation of trigonometric functions was actually inspired by watching a YouTube video hosted by an American guy who did say “coat”.
But what about the others?
cos should be “cohwse” rather than “coz”
sec should be “seek” rather than “seck”
Well, I pronounce them in the form that most closely matches the long version.
sec = seek
csc = well, I just say cosecant. I don’t ever try to shorten this one!
tan = tan
cot = coat
sin = sign
cos = coas (“coast”, but without the t)
Having said this, however, I know there are other circumstances where I’m not so consistent. So, I still understand your point even if these end up not be the best examples! 
In the UK we write cosec rather than csc, and I pronounce it “cohseck”.
Are you familiar with the hyperbolic functions: sinh, cosh, tanh, sech, cosech and coth. They’re a nightmare to pronounce. Also, ln (as in natural log).
There are actually quite a few differences in notation and terminology between the UK and US. Took me a while to realise and adapt when I worked there.
At one point in my life, yes. I would have to review. As an engineer, I had math through Calculus 3, and Differential Equations. But, being a SOFTWARE engineer, a LOT of that stuff has just fallen to distant memory!
So you’ll be at Six Flags?
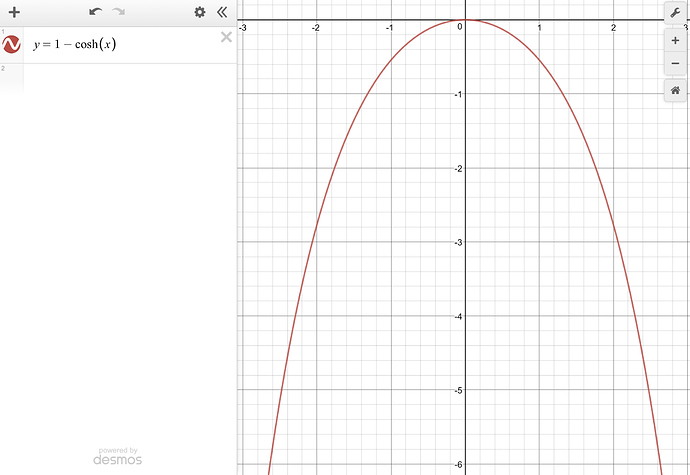
I often use US buildings as examples with my students. The Gateway Arch in St Louis, MO, is an upside-down catenary, which has equation y = cosh(x). It’s a nice example of “not all curves are parabolas”.
Wait. Are you saying that our famous landmarks are nothing but MATH EQUATIONS? 
I’m giving you a heart because I’m fond of the Arch (it’s only 15 miles away). The rest of the discussion is waaaaay over my head! I’m not that smart.